Shorter, Privacy-Preserving Proof of Reserves for Cryptocurrency Exchanges

Cryptocurrency exchanges (also called as crypto exchanges) provide a convenient way for customers to own and trade cryptocurrencies in exchange for fiat currencies. However, in cases of hacks and internal frauds in such exchanges result in huge loss of customer funds ¹^,². Proof of solvency is one of the preventive measures which could help in early detection of such scams. As a part of my master’s thesis, I am working on designing a proof of reserves for crypto exchanges wherein the exchanges can prove that they own funds enough to recover their liabilities in unfortunate cases of hack or frauds.

To illustrate the idea, let’s say an exchange owns assets equal to $v_{a}$ and has lent out crypto assets worth $v_{l}$ to its customers in exchanage for fiat currency. Thus, the liabilities of en exchange towards its cutomers is $v_{l}$ . An exchange is solvent if $v_{a} \ge v_{l}$ . A proof of reserves is a proof that an exchange owns assets equal to some amount $v_a$ . In case of crypto assets, an exchange can just reveal what addresses it owns to give a proof of its reserves. This is, however, undesirable from the point of view of privacy of the exchange’s customers. I am working on designing zero-knowledge proofs of reserves for different cryptocurrencies.

To do this without revealing the addresses and amounts, an exchange can generate two Pedersen commitments $C_a$ and $C_l$ to $v_a$ and $v_l$ respectively. To prove $v_a \ge v_l$ , exchange gives a range proof that $C_a \cdot C_l^{-1}$ is a commitment to a non-negative amount.

I am working on designing zero-knowledge proofs of reserves for different cryptocurrencies. I designed Revelio+, an efficient proof of reserves for MimbleWimble based cryptocurrencies. MimbleWimble has outputs instead of addresses to store coins. Using our protocol, an exchange proves in zero-knowledge that it owns particular outputs from the set of unspent outputs on the blockchain preserving privacy of outputs owned by an exchange. Further, it also helps detect collusion between exchanges when they try to share an output in their respective proofs of reserves.

A typical Revelio+ proof would be of the form $\Pi_{\text{Rev+}} = \{ t, I_1, I_2, \dots, I_m, \Pi_{+} \}$

where $t$ is the block height which denotes the blockchain state. All the unspent outputs $(C_1, C_2, \dots, C_n)$ on the blockchain till those included in $t$ -th block form the anonymity set. The exchange owns outputs $(C_{i_1}, C_{i_2}, \dots, C_{i_m})$ . Additionally, it defines key-images $(I_1, I_2, \dots, I_{m})$ for each output it owns. The key-images help detect collusion between exchanges, i.e. if two exchanges generate their proofs of reserves at block height $t$ and if any of their key-images match, we declare collusion. $\Pi_{+}$ is a zero-knowledge argument of knowledge which proves that the exchange actually owns the forementioned outputs. It is logarithmic in the size of set of all the unspent outputs.

Revelio, the existing protocol had a proof size linear in the size of anonymity set. Also, collusion between the exchanges could be detected only if the anonymity sets in the two proofs are the same. We alleviate both of these issues by giving a log-sized protocol and linking the proof generation with the blockchain state, we cryptographically enforce exchanges to generate proofs at the same time and thus give a foolproof way to detect collusion. Further, log-sized proof also allows us to have the anonymity set as the entire set of unspent outputs corresposing to a particular blockchain state. This enhances the privacy of exchange-owned outputs.

The downside of our protocol, however, is the time needed to generate the proof and verify the same. It is linear in the size of anonymity set size. The following graph shows the performance of our protocol in comparison to Revelio.

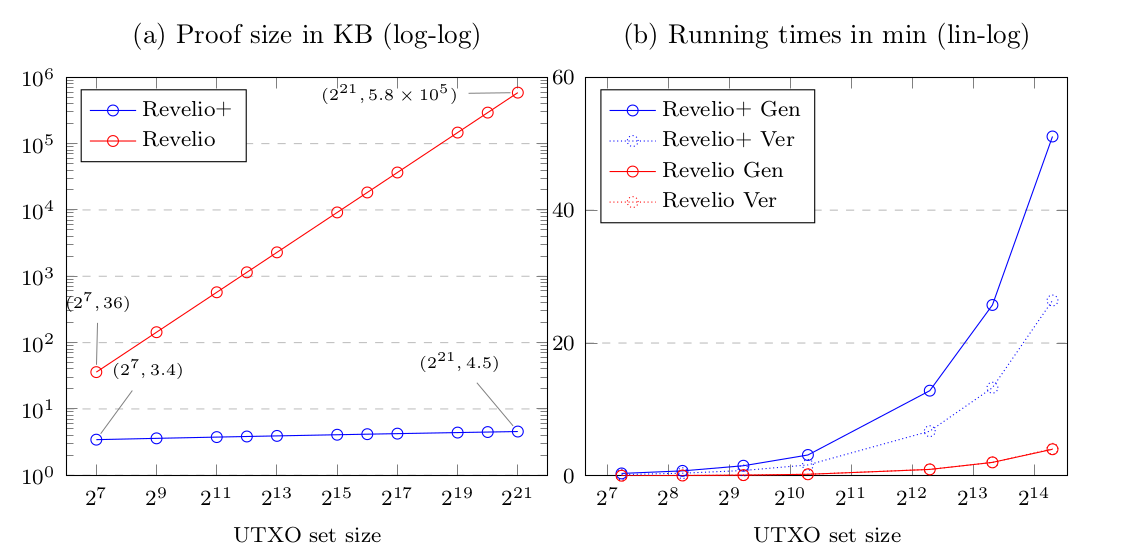
Performance comparison of Revelio and Revelio+

The linear proof generation times motivate the need for specialized hardware for cryptographic operations like elliptic curve point addition. The links for the preprint and presentation would be added soon.