In this third part on comparing Bulletproofs+ and Bulletproofs , we will delve into the math of aggregate verification of the range proofs. We compare the verification speeds of both of the protocols qualitatively as well as quantitatively. Please read blogs 1 , 2 for a primer on Bulletproofs and Bulletproofs+.
Aggregated Range Proof Protocols
An aggregated range proof implies proving that each of the quantity a j ∈ Z q a_j \in \mathbb{Z}_q a j ∈ Z q j = 1 , 2 , … , m j=1,2,\dots,m j = 1 , 2 , … , m [ 0 , 2 n − 1 ] [0,2^n - 1] [ 0 , 2 n − 1 ] crs b p = { g , h ∈ G n ⋅ m , g , h ∈ G , V = ( V 1 , V 2 , … , V m ) ∈ G m } wit b p = { a , f ∈ Z q m } stmt b p = { V j = g a j h f j and a j ∈ [ 0 , 2 n − 1 ] ∀ j ∈ [ m ] } Π b p = { A , S , T 1 , T 2 , ( L, R ) = ( L i , R i ) j = 1 log 2 ( n m ) ∈ G 2 × log 2 ( n m ) , τ , t ^ , μ , a , b ∈ Z q }
\begin{aligned}
\texttt{crs}_{bp} &= \{ \textbf{g}, \textbf{h} \in \mathbb{G}^{n\cdot m}, \ g,h \in \mathbb{G}, \ \textbf{V}=(V_1,V_2, \dots, V_m) \in \mathbb{G}^m \} \\[6pt]
\texttt{wit}_{bp} &= \{ \textbf{a}, \mathbf{f} \in \mathbb{Z}_q^m \} \\[6pt]
\texttt{stmt}_{bp} &= \{ V_j = g^{a_j} h^{f_j} \text{ and } a_j \in [0,2^{n}-1] \ \forall j \in [m] \} \\[6pt]
\Pi_{bp} &= \left\{ A,S,T_1,T_2, (\textbf{L,\ R}) = \big( L_i, R_i \big)_{j=1}^{\text{log}_2(nm)} \in \mathbb{G}^{2 \times \text{log}_2(nm)}, \tau, \hat{t}, \mu, a,b \in \mathbb{Z}_q \right\}
\end{aligned}
crs b p wit b p stmt b p Π b p = { g , h ∈ G n ⋅ m , g , h ∈ G , V = ( V 1 , V 2 , … , V m ) ∈ G m } = { a , f ∈ Z q m } = { V j = g a j h f j and a j ∈ [ 0 , 2 n − 1 ] ∀ j ∈ [ m ] } = { A , S , T 1 , T 2 , ( L, R ) = ( L i , R i ) j = 1 log 2 ( n m ) ∈ G 2 × log 2 ( n m ) , τ , t ^ , μ , a , b ∈ Z q }
Π b p + = { A , ( L, R ) = ( L i , R i ) j = 1 log 2 ( n m ) ∈ G 2 × log 2 ( n m ) , r ′ , s ′ , δ ′ ∈ Z q , A ′ , B ′ ∈ G }
\Pi_{bp+} = \left\{ A,(\textbf{L,\ R}) = \big( L_i, R_i \big)_{j=1}^{\text{log}_2(nm)} \in \mathbb{G}^{2 \times \text{log}_2(nm)}, r',s',\delta' \in \mathbb{Z}_q, A',B' \in \mathbb{G} \right\}
Π b p + = { A , ( L, R ) = ( L i , R i ) j = 1 log 2 ( n m ) ∈ G 2 × log 2 ( n m ) , r ′ , s ′ , δ ′ ∈ Z q , A ′ , B ′ ∈ G }
Note that the crs, wit, stmt \texttt{crs, wit, stmt} crs, wit, stmt
Bulletproofs Verification
Given an aggregated BP proof, a verifier needs to check the following:
g t ^ ⋅ h τ = ? g δ ( y , z ) ⋅ V z 2 ⋅ z m ⋅ T 1 x ⋅ T 2 x 2 (1)
\tag{1}
g^{\hat{t}} \cdot h^{\tau} \stackrel{?}{=} g^{\delta(y,z)} \cdot \textbf{V}^{z^2 \cdot \textbf{z}^m} \cdot T_1^x \cdot T_2^{x^2}
g t ^ ⋅ h τ = ? g δ ( y , z ) ⋅ V z 2 ⋅ z m ⋅ T 1 x ⋅ T 2 x 2 ( 1 )
verify-ipp ( g , h ′ , g x u , P h − μ g x u ⋅ t ^ , t ^ ) (2)
\tag{2}
\text{verify-ipp}(\textbf{g}, \textbf{h}', g^{x_u}, Ph^{-\mu}g^{x_u \cdot \hat{t}}, \hat{t})
verify-ipp ( g , h ′ , g x u , P h − μ g x u ⋅ t ^ , t ^ ) ( 2 )
where h ′ = ( h 1 , h 2 y − 1 , … , h m n y 1 − m n ) \textbf{h}' = (h_1, h_2^{y^{-1}}, \dots, h_{mn}^{y^{1-mn}}) h ′ = ( h 1 , h 2 y − 1 , … , h m n y 1 − m n ) P P P
P = A ⋅ S x ⋅ g − z ⋅ 1 m n ⋅ ( h ′ ) z ⋅ y m n + d (3) \tag{3} P = A \cdot S^x \cdot \textbf{g}^{-z \cdot \textbf{1}^{mn}} \cdot (\textbf{h}')^{z \cdot \textbf{y}^{mn} + \textbf{d}} P = A ⋅ S x ⋅ g − z ⋅ 1 m n ⋅ ( h ′ ) z ⋅ y m n + d ( 3 )
where d = ( z 2 ⋅ 2 n , z 3 ⋅ 2 n , … , z m + 1 ⋅ 2 n ) ∈ Z q m n \textbf{d} = (z^2 \cdot \textbf{2}^n, z^3 \cdot \textbf{2}^n, \dots, z^{m+1} \cdot \textbf{2}^n) \in \mathbb{Z}^{mn}_q d = ( z 2 ⋅ 2 n , z 3 ⋅ 2 n , … , z m + 1 ⋅ 2 n ) ∈ Z q m n ( 2 ) (2) ( 2 )
g a ⋅ s ⋅ h b ⋅ s ′ ⋅ g x u ⋅ a b = ? ( P h − μ ) ⋅ ∏ j = 1 log 2 ( n m ) L j x j 2 ⋅ R j x j − 2 (4)
\tag{4}
\textbf{g}^{a \cdot \textbf{s}} \cdot \textbf{h}^{b \cdot \textbf{s}'} \cdot g^{x_u \cdot ab} \stackrel{?}{=} (Ph^{-\mu}) \cdot \prod_{j=1}^{\text{log}_2(nm)} L_j^{x_j^2} \cdot R_j^{x_j^{-2}}
g a ⋅ s ⋅ h b ⋅ s ′ ⋅ g x u ⋅ a b = ? ( P h − μ ) ⋅ j = 1 ∏ log 2 ( n m ) L j x j 2 ⋅ R j x j − 2 ( 4 )
where s = ( s 1 , s 2 , … , s m n ) , s ′ = ( s 1 − 1 , s 2 − 1 , … , s m n − 1 ) ∈ Z q m n \textbf{s} = (s_1, s_2, \dots, s_{mn}), \textbf{s}' = (s_1^{-1}, s_2^{-1}, \dots, s_{mn}^{-1}) \in \mathbb{Z}_q^{mn} s = ( s 1 , s 2 , … , s m n ) , s ′ = ( s 1 − 1 , s 2 − 1 , … , s m n − 1 ) ∈ Z q m n i ∈ [ n m ] i \in [nm] i ∈ [ n m ]
s i = ∏ j = 1 log 2 ( n m ) x j b ( i , j ) where b ( i , j ) = { 1 if j -th bit of ( i − 1 ) is 1 − 1 otherwise
s_i = \prod_{j=1}^{\text{log}_2(nm)} x_j^{b(i,j)}
\quad
\text{ where }
\quad
b(i,j) =
\begin{cases}
1 &\text{if $j$-th bit of } (i-1) \text{ is 1} \\
-1 &\text{otherwise}
\end{cases}
s i = j = 1 ∏ log 2 ( n m ) x j b ( i , j ) where b ( i , j ) = { 1 − 1 if j -th bit of ( i − 1 ) is 1 otherwise
and ( x 1 , x 2 , … , x log 2 ( n m ) ) (x_1, x_2, \dots, x_{\text{log}_2(nm)}) ( x 1 , x 2 , … , x log 2 ( n m ) ) log 2 ( n m ) \text{log}_2(nm) log 2 ( n m ) ( 3 ) (3) ( 3 ) ( 4 ) (4) ( 4 )
g a ⋅ s ⋅ h b ⋅ s ′ ⋅ g x u ⋅ a b = ? ( A ⋅ S x ⋅ g − z ⋅ 1 m n ⋅ ( h ′ ) z ⋅ y m n + d ⋅ h − μ ⋅ g x u ⋅ t ^ ) ⋅ ∏ j = 1 log 2 ( n m ) L j x j 2 ⋅ R j x j − 2
\textbf{g}^{a \cdot \textbf{s}} \cdot \textbf{h}^{b \cdot \textbf{s}'} \cdot g^{x_u \cdot ab} \stackrel{?}{=}
\left(
A \cdot S^x \cdot \textbf{g}^{-z \cdot \textbf{1}^{mn}} \cdot (\textbf{h}')^{z \cdot \textbf{y}^{mn} + \textbf{d}} \cdot h^{-\mu} \cdot g^{x_u \cdot \hat{t}}
\right)
\cdot \prod_{j=1}^{\text{log}_2(nm)} L_j^{x_j^2} \cdot R_j^{x_j^{-2}}
g a ⋅ s ⋅ h b ⋅ s ′ ⋅ g x u ⋅ a b = ? ( A ⋅ S x ⋅ g − z ⋅ 1 m n ⋅ ( h ′ ) z ⋅ y m n + d ⋅ h − μ ⋅ g x u ⋅ t ^ ) ⋅ j = 1 ∏ log 2 ( n m ) L j x j 2 ⋅ R j x j − 2
Bringing everything to the left, we have
g a ⋅ s + z ⋅ 1 m n ⋅ h b ⋅ s ′ − z ⋅ 1 m n − ( y ′ ) m n ∘ d ⋅ g x u ( a b − t ^ ) ⋅ h μ ⋅ A − 1 ⋅ S − x ⋅ ∏ j = 1 log 2 ( n m ) L j − x j 2 ⋅ R j − x j − 2 = ? 1
\textbf{g}^{a \cdot \textbf{s} + z \cdot \textbf{1}^{mn}} \cdot
\textbf{h}^{b \cdot \textbf{s}' - z \cdot \textbf{1}^{mn} - (\textbf{y}')^{mn} \circ \textbf{d}} \cdot
g^{x_u (ab - \hat{t})} \cdot
h^{\mu} \cdot
A^{-1} \cdot
S^{-x} \cdot
\prod_{j=1}^{\text{log}_2(nm)} L_j^{-x_j^2} \cdot R_j^{-x_j^{-2}}
\stackrel{?}{=}
1
g a ⋅ s + z ⋅ 1 m n ⋅ h b ⋅ s ′ − z ⋅ 1 m n − ( y ′ ) m n ∘ d ⋅ g x u ( a b − t ^ ) ⋅ h μ ⋅ A − 1 ⋅ S − x ⋅ j = 1 ∏ log 2 ( n m ) L j − x j 2 ⋅ R j − x j − 2 = ? 1
where y ′ = ( 1 , y − 1 , y − 2 , … , y − m n + 1 ) \textbf{y}' = (1, y^{-1}, y^{-2}, \dots, y^{-mn+1}) y ′ = ( 1 , y − 1 , y − 2 , … , y − m n + 1 ) x L = ( − x 1 2 , − x 2 2 , … , − x log 2 ( n m ) 2 ) x R = ( − x 1 − 2 , − x 2 − 2 , … , − x log 2 ( n m ) − 2 ) ,
\begin{aligned}
\textbf{x}_L &= (-x_1^2, -x_2^2, \dots, -x_{\text{log}_2(nm)}^2) \\
\textbf{x}_R &= (-x_1^{-2}, -x_2^{-2}, \dots, -x_{\text{log}_2(nm)}^{-2}),
\end{aligned}
x L x R = ( − x 1 2 , − x 2 2 , … , − x log 2 ( n m ) 2 ) = ( − x 1 − 2 , − x 2 − 2 , … , − x log 2 ( n m ) − 2 ) ,
g a ⋅ s + z ⋅ 1 m n ⋅ h b ⋅ s ′ − z ⋅ 1 m n − ( y ′ ) m n ∘ d ⋅ g x u ( a b − t ^ ) ⋅ h μ ⋅ A − 1 ⋅ S − x ⋅ L x L ⋅ R x R = ? 1 (5)
\tag{5}
\textbf{g}^{a \cdot \textbf{s} + z \cdot \textbf{1}^{mn}} \cdot
\textbf{h}^{b \cdot \textbf{s}' - z \cdot \textbf{1}^{mn} - (\textbf{y}')^{mn} \circ \textbf{d}} \cdot
g^{x_u (ab - \hat{t})} \cdot
h^{\mu} \cdot
A^{-1} \cdot
S^{-x} \cdot
\textbf{L}^{\textbf{x}_L} \cdot
\textbf{R}^{\textbf{x}_R}
\stackrel{?}{=}
1
g a ⋅ s + z ⋅ 1 m n ⋅ h b ⋅ s ′ − z ⋅ 1 m n − ( y ′ ) m n ∘ d ⋅ g x u ( a b − t ^ ) ⋅ h μ ⋅ A − 1 ⋅ S − x ⋅ L x L ⋅ R x R = ? 1 ( 5 )
A verifier, thus, has to verify equations ( 1 ) , ( 5 ) (1), (5) ( 1 ) , ( 5 ) ( 1 ) (1) ( 1 ) g t ^ − δ ( y , z ) ⋅ h τ ⋅ V − z 2 ⋅ z m ⋅ ⋅ T 1 − x ⋅ T 2 − x 2 = ? 1 (6)
\tag{6}
g^{\hat{t} - \delta(y,z)} \cdot
h^{\tau} \cdot
\textbf{V}^{-z^2 \cdot \textbf{z}^m} \cdot
\cdot T_1^{-x} \cdot
T_2^{-x^2}
\stackrel{?}{=}
1
g t ^ − δ ( y , z ) ⋅ h τ ⋅ V − z 2 ⋅ z m ⋅ ⋅ T 1 − x ⋅ T 2 − x 2 = ? 1 ( 6 )
Lastly, she can combine equations ( 5 ) , ( 6 ) (5), (6) ( 5 ) , ( 6 ) c ∈ Z q c \in \mathbb{Z}_q c ∈ Z q
( g t ^ − δ ( y , z ) ⋅ h τ ⋅ V − z 2 ⋅ z m ⋅ ⋅ T 1 − x ⋅ T 2 − x 2 ) c ⋅ g a ⋅ s + z ⋅ 1 m n ⋅ h b ⋅ s ′ − z ⋅ 1 m n − ( y ′ ) m n ∘ d ⋅ g x u ( a b − t ^ ) ⋅ h μ ⋅ A − 1 ⋅ S − x ⋅ L x L ⋅ R x R = ? 1
\left(
g^{\hat{t} - \delta(y,z)} \cdot
h^{\tau} \cdot
\textbf{V}^{-z^2 \cdot \textbf{z}^m} \cdot
\cdot T_1^{-x} \cdot
T_2^{-x^2}
\right)^c
\cdot
\textbf{g}^{a \cdot \textbf{s} + z \cdot \textbf{1}^{mn}} \cdot
\textbf{h}^{b \cdot \textbf{s}' - z \cdot \textbf{1}^{mn} - (\textbf{y}')^{mn} \circ \textbf{d}} \cdot
\\
g^{x_u (ab - \hat{t})} \cdot
h^{\mu} \cdot
A^{-1} \cdot
S^{-x} \cdot
\textbf{L}^{\textbf{x}_L} \cdot
\textbf{R}^{\textbf{x}_R}
\stackrel{?}{=}
1
\\
( g t ^ − δ ( y , z ) ⋅ h τ ⋅ V − z 2 ⋅ z m ⋅ ⋅ T 1 − x ⋅ T 2 − x 2 ) c ⋅ g a ⋅ s + z ⋅ 1 m n ⋅ h b ⋅ s ′ − z ⋅ 1 m n − ( y ′ ) m n ∘ d ⋅ g x u ( a b − t ^ ) ⋅ h μ ⋅ A − 1 ⋅ S − x ⋅ L x L ⋅ R x R = ? 1
⟹ g a ⋅ s + z ⋅ 1 m n ⋅ h b ⋅ s ′ − z ⋅ 1 m n − ( y ′ ) m n ∘ d ⋅ g x u ( a b − t ^ ) + c ( t ^ − δ ( y , z ) ) ⋅ h μ + c τ ⋅ A − 1 ⋅ S − x ⋅ L x L ⋅ R x R ⋅ V − c z 2 ⋅ z m ⋅ ⋅ T 1 − c x ⋅ T 2 − c x 2 = ? 1 (7)
\tag{7}
\implies
\textbf{g}^{a \cdot \textbf{s} + z \cdot \textbf{1}^{mn}} \cdot
\textbf{h}^{b \cdot \textbf{s}' - z \cdot \textbf{1}^{mn} - (\textbf{y}')^{mn} \circ \textbf{d}} \cdot
g^{x_u (ab - \hat{t}) + c(\hat{t} - \delta(y,z))} \cdot
h^{\mu + c\tau} \cdot
\\
A^{-1} \cdot
S^{-x} \cdot
\textbf{L}^{\textbf{x}_L} \cdot
\textbf{R}^{\textbf{x}_R} \cdot
\textbf{V}^{-c z^2 \cdot \textbf{z}^m} \cdot
\cdot T_1^{-c x} \cdot
T_2^{-c x^2}
\stackrel{?}{=}
1
⟹ g a ⋅ s + z ⋅ 1 m n ⋅ h b ⋅ s ′ − z ⋅ 1 m n − ( y ′ ) m n ∘ d ⋅ g x u ( a b − t ^ ) + c ( t ^ − δ ( y , z ) ) ⋅ h μ + c τ ⋅ A − 1 ⋅ S − x ⋅ L x L ⋅ R x R ⋅ V − c z 2 ⋅ z m ⋅ ⋅ T 1 − c x ⋅ T 2 − c x 2 = ? 1 ( 7 )
Thus, an aggregated BP range proof can be verified by a single multi-exponentiation check of size 2 m n + 2 log 2 ( m n ) + m + 6 2mn + 2\text{log}_2(mn) + m + 6 2 m n + 2 log 2 ( m n ) + m + 6
Bulletproofs+ Verification
To verify an aggregated Bulletproofs+ range proof Π b p + \Pi_{bp+} Π b p + A ^ \hat{A} A ^ verify- z k - WIP \text{verify-}zk\text{-}\textsf{WIP} verify- z k - WIP
A ^ = A ⋅ g − z ⋅ 1 m n ⋅ h z ⋅ 1 m n + d ∘ y ← m n ⋅ V y m n + 1 ⋅ z 2 ⋅ z m ⋅ g ζ ( y , z ) verify- z k - WIP y ( g , h , g , h , A ^ ) (8)
\tag{8}
\hat{A} = A \cdot
\textbf{g}^{-z \cdot \textbf{1}^{mn}} \cdot
\textbf{h}^{z \cdot \textbf{1}^{mn} + \textbf{d} \circ \overleftarrow{y}^{mn}} \cdot
\textbf{V}^{y^{mn+1} \cdot z^2 \cdot \textbf{z}^m} \cdot g^{\zeta(y,z)}
\\[6pt]
\text{verify-}zk\text{-}\textsf{WIP}_{y}(\textbf{g}, \textbf{h}, g,h, \hat{A})
A ^ = A ⋅ g − z ⋅ 1 m n ⋅ h z ⋅ 1 m n + d ∘ y m n ⋅ V y m n + 1 ⋅ z 2 ⋅ z m ⋅ g ζ ( y , z ) verify- z k - WIP y ( g , h , g , h , A ^ ) ( 8 )
where ζ ( y , z ) = ( z − z 2 ) y ⋅ ⟨ 1 m n , y n m ⟩ − z y m n + 1 ⋅ ⟨ 1 m n , d ⟩ \zeta(y,z) = (z - z^2) y \cdot \langle \textbf{1}^{mn},\textbf{y}^{nm} \rangle - zy^{mn+1} \cdot \langle \textbf{1}^{mn}, \textbf{d} \rangle ζ ( y , z ) = ( z − z 2 ) y ⋅ ⟨ 1 m n , y n m ⟩ − z y m n + 1 ⋅ ⟨ 1 m n , d ⟩ y ← n m = ( y m n , y m n − 1 , … , y ) \overleftarrow{y}^{nm} = (y^{mn}, y^{mn-1}, \dots, y) y n m = ( y m n , y m n − 1 , … , y )
g e ⋅ r ′ ⋅ s ⋅ h e ⋅ s ′ ⋅ s ′ ⋅ g r ′ ⊙ s ′ ⋅ h δ ′ = ? ( A ^ ) e 2 ⋅ ( ∏ j = 1 log 2 ( n m ) L j e 2 ⋅ x j 2 ⋅ R j e 2 ⋅ x j − 2 ) ⋅ ( A ′ ) e ⋅ B (9)
\tag{9}
\textbf{g}^{e \cdot r' \cdot \textbf{s}} \cdot
\textbf{h}^{e \cdot s' \cdot \textbf{s}'} \cdot
g^{r' \odot s'} \cdot
h^{\delta'}
\stackrel{?}{=}
(\hat{A})^{e^2} \cdot
\left(
\prod_{j=1}^{\text{log}_2(nm)} L_j^{e^2 \cdot x_j^2} \cdot R_j^{e^2 \cdot x_j^{-2}}
\right) \cdot
(A')^{e} \cdot B
g e ⋅ r ′ ⋅ s ⋅ h e ⋅ s ′ ⋅ s ′ ⋅ g r ′ ⊙ s ′ ⋅ h δ ′ = ? ( A ^ ) e 2 ⋅ ⎝ ⎜ ⎛ j = 1 ∏ log 2 ( n m ) L j e 2 ⋅ x j 2 ⋅ R j e 2 ⋅ x j − 2 ⎠ ⎟ ⎞ ⋅ ( A ′ ) e ⋅ B ( 9 )
By substituting A ^ \hat{A} A ^
g e ⋅ r ′ ⋅ s ⋅ h e ⋅ s ′ ⋅ s ′ ⋅ g r ′ ⊙ s ′ ⋅ h δ ′ = ? ( A ⋅ g − z ⋅ 1 m n ⋅ h z ⋅ 1 m n + d ∘ y ← m n ⋅ V y m n + 1 ⋅ z 2 ⋅ z m ⋅ g ζ ( y , z ) ) e 2 ⋅ ( ∏ j = 1 log 2 ( n m ) L j e 2 ⋅ x j 2 ⋅ R j e 2 ⋅ x j − 2 ) ⋅ ( A ′ ) e ⋅ B
\textbf{g}^{e \cdot r' \cdot \textbf{s}} \cdot
\textbf{h}^{e \cdot s' \cdot \textbf{s}'} \cdot
g^{r' \odot s'} \cdot
h^{\delta'}
\stackrel{?}{=}
\left(
A \cdot
\textbf{g}^{-z \cdot \textbf{1}^{mn}} \cdot
\textbf{h}^{z \cdot \textbf{1}^{mn} + \textbf{d} \circ \overleftarrow{y}^{mn}} \cdot
\textbf{V}^{y^{mn+1} \cdot z^2 \cdot \textbf{z}^m} \cdot g^{\zeta(y,z)}
\right)^{e^2} \cdot
\\
\left(
\prod_{j=1}^{\text{log}_2(nm)} L_j^{e^2 \cdot x_j^2} \cdot R_j^{e^2 \cdot x_j^{-2}}
\right) \cdot
(A')^{e} \cdot B
g e ⋅ r ′ ⋅ s ⋅ h e ⋅ s ′ ⋅ s ′ ⋅ g r ′ ⊙ s ′ ⋅ h δ ′ = ? ( A ⋅ g − z ⋅ 1 m n ⋅ h z ⋅ 1 m n + d ∘ y m n ⋅ V y m n + 1 ⋅ z 2 ⋅ z m ⋅ g ζ ( y , z ) ) e 2 ⋅ ⎝ ⎜ ⎛ j = 1 ∏ log 2 ( n m ) L j e 2 ⋅ x j 2 ⋅ R j e 2 ⋅ x j − 2 ⎠ ⎟ ⎞ ⋅ ( A ′ ) e ⋅ B
⟹ g e ⋅ r ′ ⋅ s + z e 2 1 m n ⋅ h e ⋅ s ′ ⋅ s ′ − z e 2 ⋅ 1 m n − e 2 ⋅ d ∘ y ← m n ⋅ g r ′ ⊙ s ′ − e 2 ζ ( y , z ) ⋅ h δ ′ ⋅ A − e 2 ⋅ V − e 2 y m n + 1 ⋅ z 2 ⋅ z m ⋅ L x L ⋅ R x R ⋅ ( A ′ ) − e ⋅ B − 1
\implies
\textbf{g}^{e \cdot r' \cdot \textbf{s} + ze^2 \textbf{1}^{mn}} \cdot
\textbf{h}^{e \cdot s' \cdot \textbf{s}' - ze^2 \cdot \textbf{1}^{mn} - e^2 \cdot \textbf{d} \circ \overleftarrow{y}^{mn}} \cdot
g^{r' \odot s' - e^2\zeta(y,z)} \cdot
h^{\delta'} \cdot
A^{-e^2} \cdot
\\
\textbf{V}^{-e^2 y^{mn+1} \cdot z^2 \cdot \textbf{z}^m} \cdot
\textbf{L}^{\textbf{x}_L} \cdot
\textbf{R}^{\textbf{x}_R} \cdot
(A')^{-e} \cdot B^{-1}
⟹ g e ⋅ r ′ ⋅ s + z e 2 1 m n ⋅ h e ⋅ s ′ ⋅ s ′ − z e 2 ⋅ 1 m n − e 2 ⋅ d ∘ y m n ⋅ g r ′ ⊙ s ′ − e 2 ζ ( y , z ) ⋅ h δ ′ ⋅ A − e 2 ⋅ V − e 2 y m n + 1 ⋅ z 2 ⋅ z m ⋅ L x L ⋅ R x R ⋅ ( A ′ ) − e ⋅ B − 1
Note here, we have
x L = e 2 ⋅ ( − x 1 2 , − x 2 2 , … , − x log 2 ( n m ) 2 ) x R = e 2 ⋅ ( − x 1 − 2 , − x 2 − 2 , … , − x log 2 ( n m ) − 2 ) ,
\begin{aligned}
\textbf{x}_L &= e^2 \cdot (-x_1^2, -x_2^2, \dots, -x_{\text{log}_2(nm)}^2) \\
\textbf{x}_R &= e^2 \cdot (-x_1^{-2}, -x_2^{-2}, \dots, -x_{\text{log}_2(nm)}^{-2}),
\end{aligned}
x L x R = e 2 ⋅ ( − x 1 2 , − x 2 2 , … , − x log 2 ( n m ) 2 ) = e 2 ⋅ ( − x 1 − 2 , − x 2 − 2 , … , − x log 2 ( n m ) − 2 ) ,
Thus, an aggregated BP+ range proof can be verified by a single multi-exponentiation check of size 2 m n + 2 log 2 ( m n ) + m + 5 2mn + 2\text{log}_2(mn) + m + 5 2 m n + 2 log 2 ( m n ) + m + 5
Comparison of Verification Times
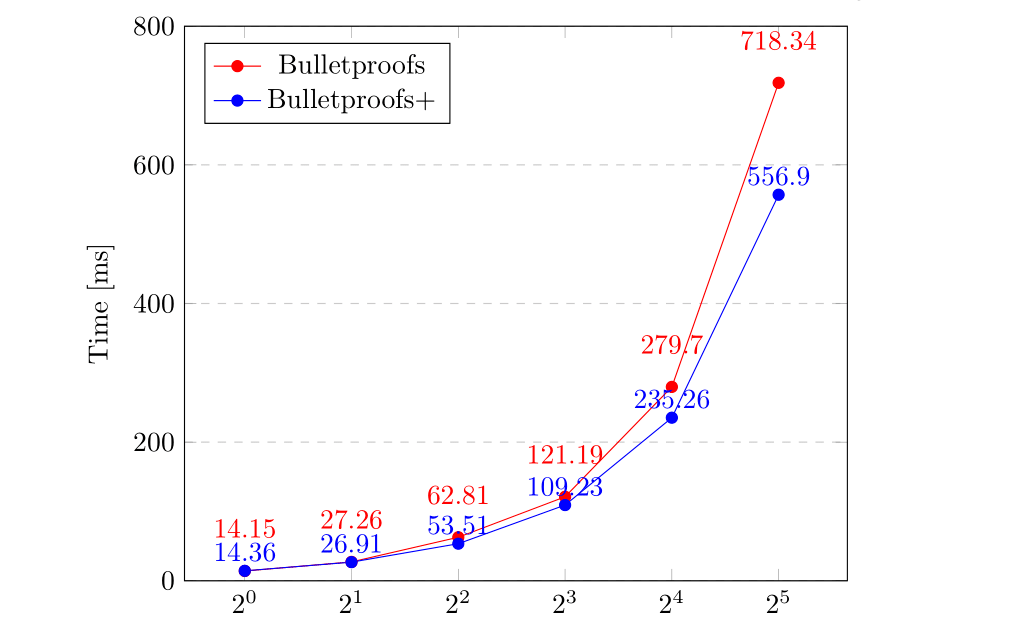
The following plot shows verification times for BP and BP+ for 64 64 6 4 secp256k1 \texttt{secp256k1} secp256k1 here .
Note that the verification speed can be further improved using Pipenger’s exponentiation algorithm for computing a multi-exponentiation.
All simulations were performed on an Intel® Core™ i7-5500U CPU running at 2.40GHz.
Plot of verification times of 64 64 6 4 m m m